Geometrie

D'Geometrie ass d'Wëssenschaft déi sech mat de Relatiounen tëscht Längten a Wénkelen am Plang oder am Raum beschäftegt. Et ass eent vun den zwee premoderne mathematesche Gebidder nieft der Léier vun den Zuelen.

Hautdesdaags ass d'Geometrie e méi ëmfangräicht Gebitt ginn. Vill Konzepter an der moderner Mathematik kënnen abstrakt a geometresche Figuren duergestallt ginn, soudatt een heiansdo guer net méi erëmkennt, datt déi nei Geometrie vun de Relatiounen tëscht Längten a Wénkele schwätzt.

Geometresch Relatiounen am Plang

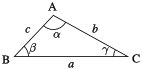
Gesetz vun de Cosinussen

och nach Relation de Pythagore généralisée genannt

$c^2=a^2+b^2-2ab\cos \gamma$

Gesetz vun de Sinussen

$\frac{\sin \gamma }{c}=\frac{\sin \beta }{b}=\frac{\sin \alpha }{a}$

Gesetz vum Thales

$\frac{OA}{OB}=\frac{A{A}^{\prime }}{B{B}^{\prime }}=\frac{O{A}^{\prime }}{O{B}^{\prime }}$

Vektoriell Relatiounen

Produit Scalaire

$\overrightarrow{AB}\cdot \overrightarrow{AC}=\Vert \overrightarrow{AB}\Vert \Vert \overrightarrow{AC}\Vert \cos \alpha$

An engem Cartesiansche Koordinatesystem wou d'Punkten A, B an C respektiv $(x_A,y_A)$, $(x_B,y_B)$ an $(x_C,y_C)$ als Koordinaten hunn, sinn d'Vecteuren $\overrightarrow{AB}$ an $\overrightarrow{AC}$ sou definéiert:
$\overrightarrow{AB}=\left(\begin{array}{c}{x}_B-x_A\\ y_B-y_A\end{array}\right)\overrightarrow{AC}=\left(\begin{array}{c}{x}_C-x_A\\ y_C-y_A\end{array}\right)$
$\overrightarrow{AB}\cdot \overrightarrow{AC}=(x_B-x_A)(x_C-x_A)+(y_B-y_A)(y_C-y_A)$

Dës Formele sinn einfach an den dräidimensionale Raum ëmzeschreiwen: et brauch ee just eng Koordinat bäizesetze wat dann erméiglegt, aus dem Plang erauszekommen. Am dräidimensionale Raum sinn d'Punkten an d'Vecteuren also duerch dräi Zuelen (hir Koordinaten) definéiert. Dat féiert dann zum Produit Scalaire am Raum:
$\overrightarrow{AB}\cdot \overrightarrow{AC}=(x_B-x_A)(x_C-x_A)+(y_B-y_A)(y_C-y_A)+(z_B-z_A)(z_C-z_A)$

Produit Vectoriel

$\overrightarrow{a}\times \overrightarrow{b}=\Vert \overrightarrow{a}\Vert \Vert \overrightarrow{b}\Vert \sin \theta \cdot \overrightarrow{n}$

Op dësem Bild kann ee gesinn datt een aus dem zweedimensionale Plang erauskënnt a sech am dräidimensionale Raum beweegt. Dofir ass och dee Vecteur $\overrightarrow{n}$ do deen gläichzäitëg e rechte Wénkel mam Vecteur $\overrightarrow{a}$ a mam Vecteur $\overrightarrow{b}$
Sief d'Vecteuren $\overrightarrow{a}=\left(\begin{array}{c}{a}_1\\ a_2\\ a_3\end{array}\right)\overrightarrow{b}=\left(\begin{array}{c}{b}_1\\ b_2\\ b_3\end{array}\right)$, dann ass $\overrightarrow{a}\times \overrightarrow{b}=\left(\begin{array}{c}{a}_2{b}_3-a_3{b}_2\\ -a_1{b}_3+a_3{b}_1\\ a_1{b}_2-a_2{b}_1\end{array}\right)$

Rotatiounen

D'Rotatiounsmatricen am dräidimensionale Raum gesi sou aus:

• Rotatioun ëm d'x-Achs

$\left(\begin{array}{ccc}1& 0& 0\\ 0& \cos \theta & -\sin \theta \\ 0& \sin \theta & \cos \theta \end{array}\right)$

• Rotatioun ëm d'y-Achs

$\left(\begin{array}{ccc}\cos \theta & 0& \sin \theta \\ 0& 1& 0\\ -\sin \theta & 0& \cos \theta \end{array}\right)$

• Rotatioun ëm d'z-Achs

$\left(\begin{array}{ccc}\cos \theta & -\sin \theta & 0\\ \sin \theta & \cos \theta & 0\\ 0& 0& 1\end{array}\right)$

Um Spaweck

• Rotation matrices at Mathworld